[데이터분석개론] PCA - Dimension Reduction 방법 중 하나

PCA ( 주성분 분석 )

Principal Component Analysis

 

- PCA 는 input variables 를 분석해서 predictors 의 갯수를 줄이는데 아주 유용한 방법이다.

 

- 데이터를 저 차원의 공간으로 project 시키는 방법이다.

  즉, N 차원의 data 를 K 차원의 data로 맵핑시키는 것이며 이때 K는 N 보다 당연히 작거나 같다.

 

- PCA는 only 숫자에만 사용이 가능하다. 따라서 카테고리형 변수는 다른 방법으로 dimension 을 줄여야한다.

 

PCA 진행 방법

 

1. X축은 dimension1 , Y축은 dimension2 에 해당하는 데이터가 산포도로 찍혀있다. 서로 음의 상관관계를 나타내고있다.

2. 컴퓨터는 이제 선 하나를 그릴건데 , 해당 선은 가장 많은 변동 ( variation ) 을 포함하도록 그려야한다.

3. 해당 선은 위 빨간 선 처럼 표시 할 수 있다. 해당 dimension 을 first principal component 이라 부른다.

4. 해당 선과 직교하는 2번째 선을 그린다. 그 dimension 을 second principal component 이라 부른다.

 

5. 위에서 그린 두가지 선( first, second principal component )을 기준으로 데이터의 산포도를 다시 그릴 수 있다.

6. 새로운 두 dimension 간의 상관관계가 0이 되었다. 즉 둘 간의 어떤 관계도 사라졌다.

 

근데 2차원→ 2차원으로 PCA 를 진행하면 차원을 줄이는 효과가 없는데 ?  라고 생각할 수 있다.

 

그림에서는 PCA는 이런방법으로 진행합니다 ~ 고 설명하기 위해서 2차원 → 2차원으로 PCA 를 진행했을뿐이고 실제 데이터의 경우는 훨씬많은 dimensions 을 가지고 있어서 당연히 dimension reduction 을 위해 PCA를 사용할 수 있다. 

 

실제 자료로 알아보는 PCA

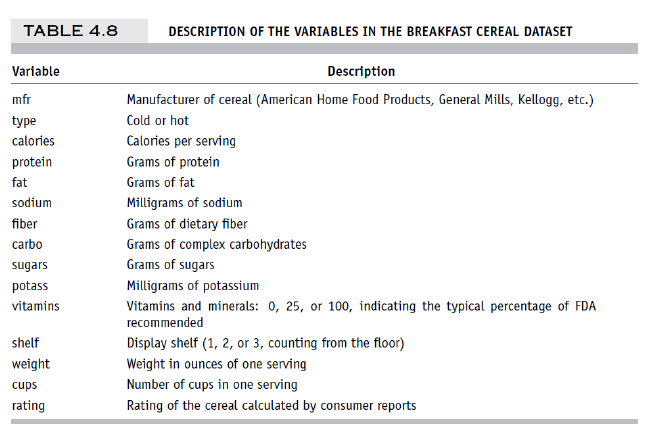
데이터를 간단하게 설명하자면 , 아침에 먹는 시리얼의 데이터 셋이다. dimension 에는 칼로리, 타입, 단백질함량, 나트륨등으로 이루어져있고 이를 기반으로한 rating 점수가 포함되어있다. 

 

( 그냥 상식적으로 예측해보자면, 단백질이나 fiber, vitamins 함량이 많을수록, 나트륨이나 칼로리는 낮을 수록 rating 이 높지않을까 ? )

 

이 수많은 차원중에는 rating 에 결정적인 차원 과 아닌 차원으로 나뉘어 질거고  , 우린 왠만하면 결정적인 애들만 데려가면서 차원을 감소시키는게 목적이다.

 

일단 설명을 위해 칼로리와 rating 만 살펴보겠다.

먼저 두 차원 간 공분산을 구해보면 위 그림처럼 나타낼수 있고,

둘 간의 상관계수를 구해보면

위 그림처럼 -0.69가 나온다. 즉 음의 상관관계를 가지고있으므로 대략적으로 칼로리가 높은 시리얼들은 rating 이 떨어진다는 결론을 얻을 수 있다.

 

러프하게 말하자면, 데이터의 전체 중 69 % 를 이 두 차원이 함께 설명하고 있으며 설명하는 변동은 음의 상관관계라고 말할 수 있다.

 

물론, 위의 공분산을 분석해보면 칼로리는 전체 변동의 66% 를 설명하고, rating 은 33%만을 설명하고있으므로 굳이 두개 중에 하나를 고르자면 더 많은 걸 설명하고있는 칼로리 라는 차원을 고르고 rating 은 버리면서 차원을 감소시킬 수 도 있다.

 

그러나 PCA는 그렇게 하지말고 적당하게 두개의 차원을 잘~ 섞어서 새로운 데이터 하나를 만들어보자 ! 가 목표라 할 수 있다.

 

Normalization 

 

그런데 이런식으로 PCA 를 하면 한가지 문제점이 있다.

 

다시 데이터셋을 살펴보자. 각 차원들의 표준편차를 살펴보면 차원마다 천차만별이다.

가령 protein 의 경우는 1.07 인것에 비해, sodium 의 경우 82.7 인것을 볼 수 있다.

 

이렇게 variance 가 서로 너무 다른데 그대로 PCA를 진행한다면 ? 

PCA는 variance 가 가장 큰 것을 잘 설명하려고 노력한다. 그래야 가장 많은 데이터를 커버할 수 있기 때문이다.

 

그럼 해당 데이터셋에는 당연히 sodium 을 중요변수로 둘 가능성이 많다. sodium 이 variance 가 가장 크기 때문이다.

즉, sodium 과 같이 애초에 variance 가 넓은 차원의 경우는 다른 차원보다 PCA에 있어서 유리한 점이 있고,

반대로 말하면 protein 과 같이 애초에 variance 가 좁은 차원의 경우는 다른 차원보다 PCA에 있어서 아주 불리하다는 것이다.

 

때문에 이 표준편차들을 전부 고만고만하게 normalization 하는 과정이 필요하다. 그래야 차원끼리 공정하게 싸울 수 있으므로 !

 

normalization 은 mean 과 variance 를 표준 정규분포로 맞춰주면 된다.

즉, 평균은 0에 수렴하도록, 분산은 1에 수렴하도록 바꿔주자 !

 

 

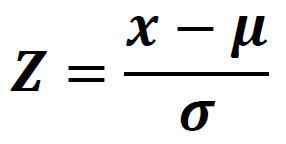
전처리를 하지 않은 데이터셋에서 차원끼리 표준편차가 일정한 경우는 거의 존재하지 않는다. 

때문에 데이터를 처음 가져와 PCA를 사용할 경우에는 꼭 ! Normalization 과정을 거쳐주자 !

 

위 그림은 Normalization 을 사용하지않고 PCA를 한 모습이다.

총 10가지 차원 중에서 두가지 차원만으로 92%에 해당하는 데이터가 설명이 가능한데, 이는 정규화를 진행하지 않은탓에 두가지 차원의 variance 가 너무 커서 왜곡이 일어났을 뿐 , 정확한 분석이라고 할 순 없다.

 

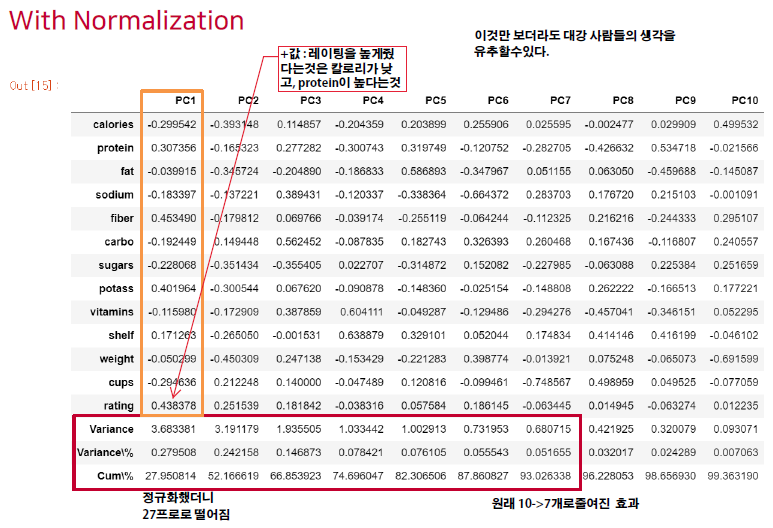
위 그림은 정규화를 수행 후 PCA를 한 모습이다. 

정규화를 수행했을때와는 다르게 sodium 의 가중치가 확 내려간것을 볼 수 있다. 

총 데이터의 93%정도를 설명하려면 최소한 새로운 차원 7 개 정도는 필요한 걸 볼 수 있다. ( 보통 90% 가 넘어가는 선에서 PC 개수를 정하곤 한다. )

 

예상대로 protein 과 rating 이 양의 상관관계를 가지고 있고, sodium 과는 음의 상관관계를 가지고 있음도 확인할 수 있다.

 

 

 

오랜만에 데이터분석개론을 복습하니까 기억이 새록새록 아주 재밌다 !

얼른 개념정리를 끝내고 다시 Python 을 한번 다뤄봐야겠다 ㅎㅎ