[알고리즘] Level3 ) 섬 연결하기 - C++

Level 3으로 올라오니 확 어려워진 느낌이 든다.

상식으로 풀기보다 문제를 읽고 아 ! 이건 어떤 알고리즘으로 접근하면 되겠다.

라는 생각이 들도록 노력해야겠다.

 

무튼 이번 문제는 수업때 듣고 이제는 기억이 가물가물한.. 최소신장트리를 이용한 문제다.

 

문제 설명

 

n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.

다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.

 

제한사항

• 섬의 개수 n은 1 이상 100 이하입니다.
• costs의 길이는 ((n-1) * n) / 2이하입니다.
• 임의의 i에 대해, costs[i][0] 와 costs[i] [1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i] [2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
• 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
• 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
• 연결할 수 없는 섬은 주어지지 않습니다.

입출력 예

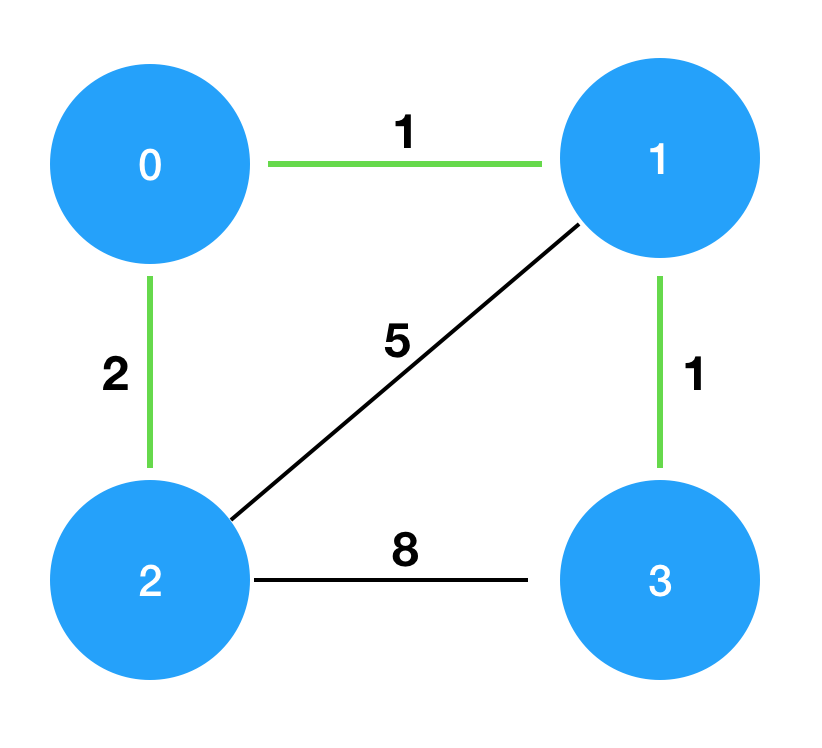
4

[[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]]

4

입출력 예 설명

costs를 그림으로 표현하면 다음과 같으며, 이때 초록색 경로로 연결하는 것이 가장 적은 비용으로 모두를 통행할 수 있도록 만드는 방법입니다.

접근방법

 

앞에서 말했듯이 '최소신장트리' 를 이용하면 쉽게 풀 수 있는 문제였다.

최소신장트리를 구현하는 방법에는 두가지 방법이 있는데 나는 크루스칼 알고리즘으로 접근해봤다.

 

구현

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int parent[100];

class Edge {
public:
	int node[2];
	int cost;
	Edge(int a, int b, int cost) {
		this->node[0] = a;
		this->node[1] = b;
		this->cost = cost;
	}

	//간선을 오름차순으로 정렬할때 기준을 cost로 정함.
	bool operator<(Edge &edge) {
		return this->cost < edge.cost;
	}

};

//재귀로 구현한 부모노드 가져오는 함수
int getParent(int node) {
	if (parent[node] == node) return node;
	else return getParent(parent[node]);
}

// 노드끼리 연결시키는 함수. 이때 부모노드는 작은 노드로 쓴다.
void unionParent(int node1, int node2) {
	node1 = getParent(node1);
	node2 = getParent(node2);
	if (node1 < node2) parent[node2] = node1;
	else parent[node1] = node2;
}

// 사이클인지 판단하는 함수
bool isCycle(int node1, int node2) {
	node1 = getParent(node1);
	node2 = getParent(node2);
	if (node1 == node2) return true;
	else return false;
}

int solution(int n, vector<vector<int>> costs) {
	int answer = 0;
	vector<Edge> v;
	for (int i = 0; i < costs.size(); i++) {
		v.push_back(Edge(costs[i][0], costs[i][1], costs[i][2]));
	}

	sort(v.begin(), v.end());

	//각 노드는 자기자신이 부모로 초기화해줍니다. 
	for (int i = 1; i <= n; ++i) {
		parent[i] = i;
	}
	for (int i = 0; i < v.size(); i++) {
		//싸이클이 존재하지 않으면 비용을 더합니다. 
		if (isCycle(v[i].node[0], v[i].node[1]) == false) {
			answer += v[i].cost;
			unionParent(v[i].node[0], v[i].node[1]);
		}
	}
	return answer;
}

 

기억할 점

 

클래스를 정의하는 부분 ! 오랜만에 봐서 찾아보면서 적었다 . 기억해두자

특히 c++ 에서 sort 할때 sort를 기준을 정의하는 부분은 계속 까먹는다. 기억해두자

재귀함수는 코드를 보면 쉬운데 내가 짜는건 어렵다... !