[데이터분석개론]Cluster Analysis

Classification VS Clustering 

 

Classification : 과거에 이 데이터가 어떤 클래스에 소속되어있었다 ! 라는게 존재. 즉 지도학습

Clustering : 이런 정보 자체가 없다. 즉 비지도 학습으로 분류할 y값이 정해져있지 않고 컴퓨터가 알아서 데이터 기준으로 분류한다. 즉 비지도학습

 

 

Clustering

 

미국의 22개의 public utilities 에 대한 데이터 자료다.

fuel cost 와 sales 을 y축과 x 축으로 가지는 산점도를 그려보면 이렇게 나타 날 수있는데

우리는  이 산점도를 보고 대략적으로 3 그룹으로 나눌 수있다.

여기서 이렇게 원으로 잘 묶는것, Pacific 같은경우 빨간 원과 노란 원의 경계 즈음에 위치하는데, 이 판단을 정확히 해주는 것이 바로 clustering 이다.

 

Clustering 의 타입

• Hierarchical clustering : 데이터 간 계급을 나눌 수 있다.
  • Agglomerative 방식 이용 : 가장 작은 단위부터 하나씩 뭉쳐나가는 것
  • Divisive 방식 이용 : 가장 큰 것에서 잘라나가는 것
• Non-hierarchical clustering : 계층구조 없이 데이터는 모두 평등하다고 가정한다. ex) K-means Clustering

 

Clustering 의 기준

 

레코드 간 distance 로 측정.

 

 

 는 레코드 i 와 레코드 j 사이의 거리를 나타내는데,  레코드 i 와 j 는 각각 p 개의 measurements 로 이루어져있다.

는 4가지 속성을 가지고 있다.

 

• Non-negative : 거리를 나타내므로 항상 양수 값을 가진다.
• Slef-proximity : 자기 자신과의 거리는 0이다.
• Symmetry : i와 j 사이의 거리 = j 와 i 사이의 거리
• Triangle inequality : 피타고라스의 정리를 생각하면 쉽다.

레코드 간  distance 를 구하는 방법

• Euclidean Distance 

KNN 알고리즘에서 살펴본 유클리디안 거리를 사용해서 구한다.

이때는 scales 보정을 위해 normalization 이 필요하고 , outlier 에 민감하게 반응하기때문에 이 outlier 를 잘 제외시켜줘야한다.

 

• Correlation-based Similarity 

correlation dl [ -1 ~ +1 ] 사이의 값을 가진다고 배웠다.

correlation 이 1에 가까울 수록 i 와 j 가 엄청 비슷하다는걸 뜻한다. 

바로 이 correlation 을 이용해서 distance 를 구할 수 있다.

• Manhattan Distance ( City Block )

유클리드 거리에선 서로 뺀값의 제곱의 루트를 씌워주는 형태로 음수값을 제거했는데, 

맨하탄 거리의 경우 뺸값의 절댓값을 씌워주는 것으로 음수값을 제거한다.

 

때문에 이 맨하탄 거리를 이용하면 서로간 level 차이를 더 뚜렷하게 볼 수있다.

 

클러스터 간  distance 를 구하는 방법

 

위의 그림처럼 컴퓨터가 실제로 원 모양을 그려주면 좋겠지만 , 컴퓨터는 이 원을 그려주지 않는다. 

때문에 원 사이 간, 즉 클러스터 간 사이의 거리를 측정할땐 클러스터 안의 데이터 간 거리로 측정해줘야 한다.

 

• Minimum Distance : A 클러스터의 데이터 , B 클러스터의 데이터 중 가장 가까운 것 간의 거리
• Maximum Distance : A 클러스터의 데이터,  B 클러스터의 데이터 중 가장 먼 것 간의 거리
• Average Distance : 데이터 별로 모든 거리를 구한 후에 그 평균 값
• Centroid Distance : A 클러스터의 center , B 클러스터의 center 사이의 거리

 

Hierarchical Agglomerative Clustering

 

1. 몇개의 클러스터로 나눌 지 정한다.

2. 가장 가까운 두개의 records 를 하나의 클러스터로 묶는다.

3. 그 다음 가장 가까운 두개의 records 를 하나의 클러스터로 묶는다.

4. 2,3 과정을 반복한다.

 

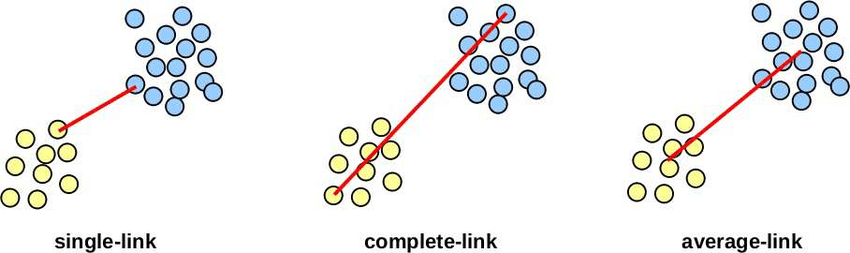
Linkage ( 묶는 방법 )

• Single Linkage : minimum distance 를 사용해서 묶는다
• Complete Linkage : maximum distance 를 사용해서 묶는다.
• Average Linkage : average distance 를 사용해서 묶는다.

 

Dendrograms 

클러스터로 묶고, 또 묶고 하는 과정을 다이어그램으로 나타낸 것.

즉 클러스터링 과정을 나타내는 다이어그램이다.

 

Y축의 값이 크면 클수록 서로 거리 차이가 난다는걸 의미하며,

결국에는 NY 와 나머지 클러스터가 묶이면서 총 1개의 클러스터로 다 묶이게 되는 걸 볼 수 있다.

위로 갈수록 하나의 records 와 나머지 클러스터 끼리 묶이는 경향이 있는 걸 볼 수 있는데, 

이는 이 데이터 셋이 클러스터링 하긴 좋지않은 데이터셋임을 나타낸다.

보통은 클러스터 와 클러스터 간으로 묶여야 그 고리만 잘라내면 우리가 생각하는 클러스터로 분리할 수 있기 때문이다.

 

 

Validating Clusters 

 

클러스터링을 할땐 의미가 있는 클러스터로 분류하는게 중요하다.

• Cluster interpretability : 클러스터가 의미가 있어서 labeling 을 할 수 있어야한다. 예를들어 아 이 클러스터는 수익을 많이내는 회사를묶은 클러스터다 ~ 이런식으로 !
• Cluster stability : 클러스터가 안정적인가 ? input을 좀 바꿨는데 클러스터가 확 달라진다면, 그건 안정성있는 클러스터가 아니다.
• Cluster separation : 클러스터끼리 잘 나누어져 있는가 ? 만약 클러스터 안에있는 데이터들 간 평균거리를 구해봤는데 다른 클러스터에 비해 상대적으로 너무 크다면 이걸 클러스터라고 말할 수 있는지 생각해봐야 한다.
• Number of Clusters : 그래서 몇개로 클러스터를 나눌 지 어떻게 결정할 것인가 ? 이게 Key point 이다 !

Limitations of Hierarchical Clustering

• Hierarchical Clustering 의 경우엔 데이터 숫자가 많으면 엄청나게 많은 계산량을 요구한다. 레코드간 모든 distance 를 다 구해야 하기 때문이다.
• Hierarchical Clustering 의 경우엔 레코드를 딱 한번만 할당하므로 ,만약 잘못 할당된 경우엔 되돌릴 수 없다.
• 낮은 안정성을 가진다. distance를 어떤 방식으로 구하냐에 따라 cluster 가 확확 바뀌곤 한다. 이게 가장 큰 문제점인데 보통 outliers 때문에 발생하므로 전처리과정에서 outliers 를 잘 골라내야 한다.

 

K-means Clustering 

계층구조가 없이 모든 데이터를 평등하다고 생각하는 non-hierarchical clustering 의 대표적인 방법이다.

K 는 클러스터의 갯수를 의미하며, 무조건 시작할때 이 K 를 정해두고 시작해야한다.

Hierarchical Clustering 의 경우, 덴드로그램을 다 그려놓고 K 를 정하는 것과 대비된다.

 

1. K 값을 선택한다.

2. 매 step 마다 임의의 점을 찍고, 그 점을 중심으로 클러스터를 나눈다.

3. 컴퓨터가 이 중심점을 계속 움직여가면서 가장 최소의 distance 합을 가지는 중심점을 찾는다.

4. 2,3 과정을 반복한다.

 

중심점을 찾고, 또 이 중심과 데이터간의 거리를 구하고 다시 중심점을 찾는 과정을 반복해가면서

클러스터링을 하는 과정이다.

 

Choosing K

K-means Clustering 에서는 이 K 값을 잘 선택하는게 중요하다.

 

• K 값이 너무 작은경우

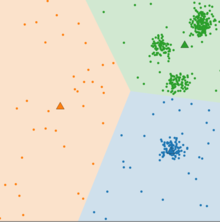
위의 그림은 K=3 일때를 나타낸다. K 값이 너무 작아서 주황색 클러스터의 경우엔 클러스터라고 말하기 뭐한 ? 클러스터로 결과가 나왔다.

 

• K 값이 너무 큰 경우

반대로 K=8 로 정해버리면 너무 세세하게 나눠서 클러스터의 의미가 사라진다.

 

그럼 어떻게 K 값을 적당하게 구할 수 있을까 ?

해당 그래프는 K 별 클러스터 안에있는 거리들의 제곱 평균을 나타내는 그래프다.

K=1인경우 모든 데이터를 하나의 클러스터로 묶기때문에 아주 높은 distance를 보이고,

K 가 커지면 커질수록 클러스터를 점점 쪼개기때문에 거리가 줄어든다.

K 를 데이터 숫자만큼 설정하면 , 데이터 하나하나가 각각의 클러스터가 되는거고 거리는 0 에 수렴한다.

 

때문에 이 빨간박스친 이 구간 즈음에서 K 값을 정해주는데, 이를 팔꿈치 같다고 해서 elbow point 라고 부른다.

 

 

K-means Clustering  의 한계

• 처음 중심이 랜덤배정인데, 데이터가 많은 경우 첫 시작이 어디냐에 따라서 결과가 크게 다르게 나온다.
• 매번 할때마다 결과가 달라서 신뢰할수있느냐의 문제가 발생하므로, 각 K에 대해 여러번 반복해서 결과를 도출해야한다.
• 따라서 내가 어떤 문제에 대해서 어떠한 정보도 알 수 없을때 대충 파악하는 정도로 사용하면 아주 좋은 방법이다.